2.KMP算法
2.1. KMP算法
求解问题:有两个字符串str1和str2,寻找str1是否包含str2,并找出包含的起始位置。如str1=12341234d,str2=1234d,则包含的起始位置为4。
笨办法:假设str2的字符串长度为m,从str1的0位置开始,选取以该位置开头的长度为m的子字符串与str2匹配,若匹配成功,返回该位置,若匹配不成功,则从str1的下一个位置开始继续匹配,直到匹配结束。
KMP算法:(时间复杂度O(n))
a) 利用str2建立长度为m的next数组,表示str2对应位置前面字符串的最大前缀和最大后缀的匹配。
建立规则:取str2的第i个字符,看str2(i)前面的子字符串,其中前缀与后缀相等时的最大长度。其中前缀不能包括子字符串的最后一位,后缀不能包括子字符串的第一位。Next数组以-1和0开头。
举例:str2=12341234d,
| 前后缀长度 | 前缀 | 后缀 |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 12 | 34 |
| 3 | 123 | 234 |
| 4 | 1234 | 1234 |
| 5 | 12341 | 41234 |
| 6 | 123412 | 231234 |
由上表可知,当长度为4时,前缀与后缀相等,为1234。故该点的next数值为4。
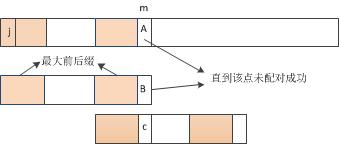
b) 建立好str2的next数组时,还是以str1的0位置开始与str2配对,假设在以str1的j位置开始与str2配对时,直到m位置未配对成功,此时str2的m位置最大前后缀为下图橙色区域,橙色区域位置字符串均相等,则下次配对str2直接右移至下图位置,可直接比较C与A是否相等。
1 | /** |
2.2. KMP算法扩展题目一
给定一个字符串str1,只能往str1的后面添加字符变成str2。
要求1:str2必须包含两个str1,两个str1可以有重合,但是不能以同一个位置开头。
要求2:str2尽量短。
要求返回str2。
举例:
str1=123,str2=123123,包含两个str1,且不以相同位置开头,且str2最短。
str1=123123,str2=123123123,包含两个str1,且不以相同位置开头,且str2最短。str1=111,str2=1111,包含两个str1,且不以相同位置开头,且str2最短。
解法:求str1最后一个字符后一个位置的next数值,然后把str1除去最大前缀的剩下字符串放在str1后面就形成str2。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28/**
* 给定一个字符串str1,只能往str1的后面添加字符变成str2。
* 要求1:str2必须包含两个str1,两个str1可以有重合,但是不能以同一个位置开头。
* 要求2:str2尽量短。
* 要求返回str2。
* @param str1
* @returns {string}
*/
function kmpQuestion1(str1) {
var next = new Array(str1.length+1);
var pos = 2;
var cn = 0;
var arr1 = str1.split('');
next[0] = -1;
next[1] = 0;
//求next数组
while(pos<arr1.length+1){
if(arr1[pos-1]===arr1[cn]){
next[pos++]=++cn;
}else if(cn>0){
cn=next[cn];
}else{
next[pos++]=0;
}
}
return str1+str1.substring(cn);
}
console.log(kmpQuestion1('123123'));//123123123
2.3. KMP算法扩展题目二
给定两个二叉树T1和T2, 返回T1的某个子树结构是否与T2的结构相等。
解法:将两个二叉树分别序列化,然后判断T1字符串中是否包含T2字符串。


